Toute déviation de la norme sera punie, sauf si elle est exploitable
LA PLANCHE DE GALTON
Vous devez tirer le premier coup au billard anglais (8 Pool) et pour ce faire tapez avec la pointe d’un bâton (la queue) une grosse bille blanche pour que celle-ci aille percuter un groupe de 15 billes colorées disposées en triangle, une pointe vers vous, situées de l’autre côté de la table. Vous savez qu’une infime variation de votre frappe, tant en vitesse qu’en positionnement, modifiera totalement la répartition des billes après le choc. Alors vous réfléchissez un peu. Vous vous dites que si on remplaçait les billes du triangle par un matériau dur, alors une infime variation de votre geste déciderait si la bille blanche va à droite ou à gauche, c’est-à-dire a un comportement ou un autre qui sont complètement opposés. C’est pire que l’Effet Domino : un rien transforme totalement l’avenir. Est-ce toujours le cas ? Notre vie n’est-elle qu’une succession de ces “décisions” ? Que se passe-t-il quand elles se succèdent directement ?
Pour le savoir, vous vous lancez dans le bricolage. Vous prenez une planche, la posez verticalement contre un mur, et y plantez des clous de telle sorte à ce qu’ils obligent une bille tombant à devoir à chaque fois aller à droite ou à gauche : un sur la première ligne, deux sur la deuxième, etc. Vous devez être extrêmement précis : la validité votre modélisation en dépend. Mais heureusement vous découvrez que vous pouvez ranger votre attirail : un tel dispositif existe déjà, et on peut même l’acheter et en voir des vidéos en ligne. C’est la Planche de Galton, du nom de son inventeur Sir Francis Galton (1822–1911). Dès lors vous savez ce qui va se passer : si vous lâchez une bille unique, elle va arriver plus ou moins à gauche ou à droite du bas de la planche, mais si vous en lâchez beaucoup, alors elles vont préférentiellement s’empiler vers le milieu de la planche, et dessiner ainsi une forme célèbre, la Courbe en Cloche (Bell Curve).
L’explication de la Planche de Galton est simple : la courbe montre les nombres de trajets permettant d’atteindre chaque case du bas. Mais cet effet est généralisable : dès lors qu’il y a suffisamment de facteurs en jeu pour que les biais se compensent, le résultat approxime une Loi Normale, qui est représentée par une courbe en forme de cloche.
LA COURBE EN CLOCHE
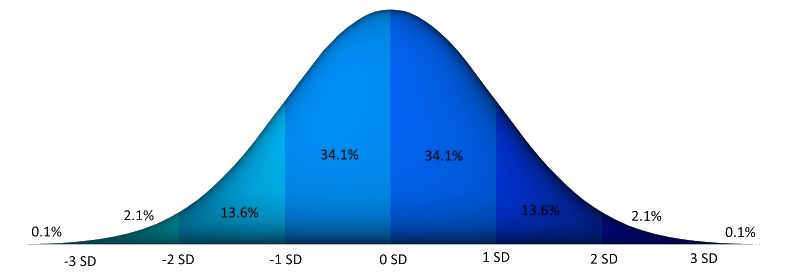
Il existe de très nombreuses “Lois” en statistiques, qui décrivent comment une population est répartie (distribuée). La Loi Normale (dite aussi Loi de Gauss), qui se représente graphiquement par une “Courbe en cloche” (aussi appelée “Gaussienne”), offre les avantages d’être particulièrement simple à comprendre intuitivement et d’être symétrique. Il suffit en effet de connaître sa Moyenne (ou Espérance) et son Écart-Type pour la définir complètement. L’Ecart-Type (en anglais : Standard Deviation ou “SD”, noté sigma minuscule : σ) est défini comme la Racine Carrée de la Moyenne des Carrés des Écarts ce qui pour un mathématicien ou un ordinateur est vraiment très simple. Visuellement, il correspond à la valeur où la courbe change d’orientation, et plus il est élevé plus la courbe apparaît aplatie. Cet écart-type nous permet de déterminer précisément quel pourcentage de la population étudiée est à telle ou telle valeur, ce qui signifie précisément que dès qu’un phénomène dépend de multiples facteurs suffisamment indépendants, on peut très facilement déterminer la répartition des valeurs de ce phénomène, combien sont à tel ou tel niveau. Cet avantage est exploité en permanence dans tous les domaines. Par exemple, sauf précision contraire, la célèbre “Marge de confiance” de 95% (ou “Marge d’erreur” de 5%) correspond à 2 écarts-types d’écart dans une Loi Normale.
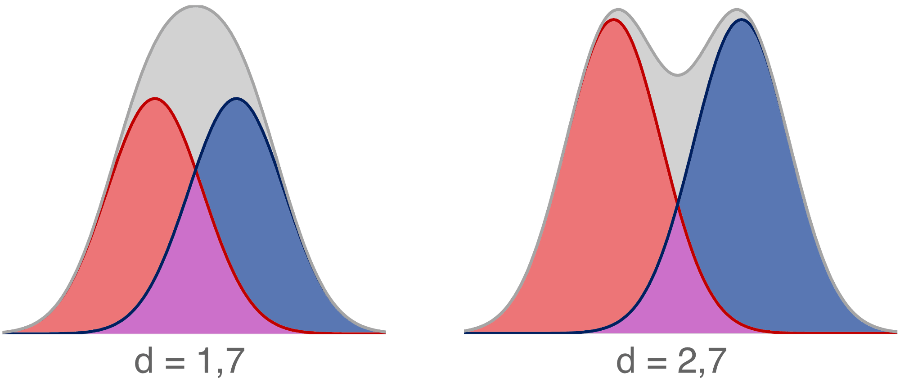
Comme indiqué dans la Base Eco 12, on peut aussi s’intéresser à l’addition de plusieurs courbes en cloches. Par exemple on peut vouloir comparer la distribution selon le sexe ou selon l’âge. Est-ce que l’addition de deux courbes donne aussi une courbe en cloche ? En d’autres termes : une courbe en cloche peut-elle être l’addition de deux ou plusieurs courbes en cloche ? En fait oui, souvent : il faut que l’écart entre les moyennes soit supérieur à deux écarts-types pour qu’une addition montre une courbe à deux bosses (Schilling et al. 2002). Pourtant, ce niveau d’écart est déjà énorme : seulement 2,3% d’une des sous-populations dépasse le niveau moyen de l’autre.
QUI EST NORMAL ?
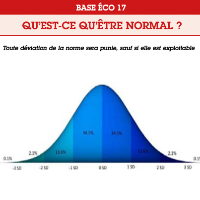
Dès lors nous pouvons définir ce qu’est la normalité : c’est être dans la norme, c’est-à-dire à moins d’un écart-type de la moyenne sur un critère suivant la Loi Normale dans une population définie. En d’autres termes : 68,2% de cette population est normale sur ce critère.
Au sein de la population humaine, nous sommes tous normaux sur la plupart des critères qui nous définissent (taille, poids, santé, etc.) dans notre groupe usuel. Mais le simple fait d’être anormaux (à plus de 1 écart-type de la moyenne) sur quelques autres suffit à nous rendre, tous, uniques. C’est cette opposition qui explique pourquoi il est beaucoup plus facile de manipuler les foules, que ce soit pour des objectifs commerciaux ou politiques, qu’un individu unique : c’est elle qui fonde tout le marketing.
La normalité n’a rien à voir avec la moralité, elle n’est qu’une caractéristique statistique.
Philippe Gouillou
Références : Base Eco 12 ; Henrich et al. (2010, doi:10.1017/S0140525X0999152X) ; Neuromonaco 33 ; Schilling et al. (2002, doi:10.1198/00031300265) ; Wikipedia : Planche de Galton
Image : Galton Box by Matemateca (IME/USP)/Rodrigo Tetsuo Argenton. Licence CC-BY-SA 4.0*